The brand manager for a brand of toothpaste must plan a campaign designed to increase brand recognition. He wants to first determine the percentage of adults who have heard of the bran. How many adults must he survey in order to be 90% confident that his estimate is within seven percentage points of the true population percentage?
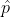 = 0.5
= 0.5
1 -
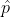 = 0.5
= 0.5
margin of error (E) = 0.07
At 90% confidence level the t is,
alpha = 1 - 90%
alpha = 1 - 0.90
alpha = 0.10
alpha / 2 = 0.10 / 2 = 0.05
Zalpha/2 = Z0.05 = 1.645
sample size = n = (Z
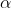 / 2 / E )2 *
/ 2 / E )2 *
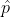 * (1 -
* (1 -
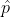 )
)
= (1.645 / 0.07)^2 *0.5*0.5
23.5^2 * 0.5 * 0.5
552.25 * 0.5 * 0.5
= 138.06
sample size = 138
He must survey 138 adults in order to be 90% confident that his estimate is within seven percentage points of the true population percentage.
1 -
margin of error (E) = 0.07
At 90% confidence level the t is,
alpha = 1 - 90%
alpha = 1 - 0.90
alpha = 0.10
alpha / 2 = 0.10 / 2 = 0.05
Zalpha/2 = Z0.05 = 1.645
sample size = n = (Z
= (1.645 / 0.07)^2 *0.5*0.5
23.5^2 * 0.5 * 0.5
552.25 * 0.5 * 0.5
= 138.06
sample size = 138
He must survey 138 adults in order to be 90% confident that his estimate is within seven percentage points of the true population percentage.